VITEEE 2015 :: Physics :: General questions

• Physics - General questions

The capacitance of a parallel plate capacitor with air as a medium is 3 $\mu$ F. As a dielectric is introduced between the plates, the capacitance becomes 15 $\mu$ F. The permittivity of the medium C²N^-1 m^-2 is 

Answer:

Explanation:

 Capacitance  of air capacitor 

 $C_{0}= \frac{\epsilon_{0}A}{d}=3\mu F$  ....(i)

 whem a dielectric of permittivity $\epsilon_{r}$ and dielectric constant K  is introduced between the plates , then 

 Capacitance  ,  $C= \frac{k\epsilon_{0}A}{d}=15\mu F$  ...(ii)

 Dividing eq.(ii)  by (i)  , we get

 $\frac{C}{C_{0}}=\frac{d}{\frac{k\epsilon_{0}A}{d}} =\frac{15}{3}$

 $\Rightarrow$  K=5

 $\therefore$  permittivitty of the medium

 $\epsilon_{r}=\epsilon_{0}K$

 =  $8.85\times 10^{-12}\times 5=0.44\times 10^{-10}$

A condenser of capacitance  C is fully charged by a 200V supply. It is then discharged through a small coil of resistance wire embedded in a thermally insulated block of specific heat 250 J/kg-K and of mass 100 g. If the temperature of the block rises by 0.4 K, then the value of  C is 

Answer:

Explanation:

 The energy stored in the capacitor

$U= \frac{1}{2}CV^{2}=\frac{1}{2}C\times(200)^{2}=2 C\times 10^{4} J$

 This  energy is used to heat up the block 

Let  $\triangle\theta$ be the rise in temperature , then  heat energy

 $Q=ms\triangle\theta=0.1 \times 250\times0.4=10 J$

 Now  $2 C\times 10^{4}=10$

 $\Rightarrow$     $C= \frac{10}{2\times 10^{4}}=5\times 10^{-4}=500\mu F$

Two points masses, m each carrying charges -q and +q are attached to the ends of a massless rigid non-conducting wire of length  'L'  . when this arrangement is placed in the uniform electric field, then it deflects through an angle i. The  minimum time  needed by rod to  align itself  along the field is 

Answer:

Explanation:

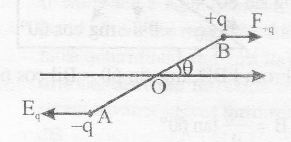
Torque  when the wire is brought in a uniform field E

$\tau= qEL\sin\theta$

= $ qEL\theta$       [ $\because$ $\theta$  is very small]

Moment of intertia  of rod AB about O

$I=m\left(\frac{L}{2}\right)^{2}+m\left(\frac{L}{2}\right)^{2}=\frac{mL^{2}}{2}$

$\tau= I\alpha$

$\therefore$     $\alpha=\frac{\tau}{I}=\frac{qEL\theta}{\frac{mL^{2}}{2}}$

$\Rightarrow $    $\omega^{2}\theta=\frac{2qEL\theta}{mL^{2}}[\because \theta=\omega^{2}\theta]$

$\Rightarrow \omega^{2}=\frac{2qE}{mL}$

 Time period of the wire

$T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{mL}{2qE}}$

The rod will become parallel to the field

in time T/4

$\therefore$     $t=\frac{T}{4}=\frac{\pi}{2}\sqrt{\frac{mL}{2qE}}$

Equal charges q each are placed at the vertices of an equilateral triangle of side r. The magnitude  of electric  field intensity at any vertex is 

Answer:

Explanation:

 Due to charge  at A and B magnitude of intensity of electric field at point C

$E_{1}=E_{2}=\frac{1}{4\pi\epsilon_{0}}.\frac{q}{r^{2}}$

 Net intensity at point C is

 $E_{R}=\sqrt{E_{1}^{2}+E_{2}^{2}+2E_{1}E_{2}\cos 60^{0}}$

$E_{R}=\sqrt{E_{1}^{2}+E_{2}^{2}+2E_{1}^{2}\times\frac{1}{2}}=\sqrt{3}E_{1}=\frac{\sqrt{3}q}{4\pi \epsilon_{0}r^{2}}$

When the momentum of a photon is changed by an amount p' then the corresponding change in the de-Broglie wavelength is found to be 0.20%. Then the original moment of the photon was

Answer:

Explanation:

As, we know de-Broglic  wavelength

 $\lambda=\frac{h}{p}$

$\therefore$     $\lambda\propto\frac{1}{p}$

$\Rightarrow \frac{\triangle p}{p}=-\frac{\triangle \lambda}{\lambda}\therefore |\frac{\triangle p}{p}|=|\frac{\triangle \lambda}{\lambda}|$

$\Rightarrow \frac{p'}{p}=\frac{0.20}{100}=\frac{1}{500}$

 or, p=500 p'

• Physics - General questions